Схематизация опорных устройств

20. Область применения сварных конструкций

21. Конструкции сварных соединений

22. Расчет на прочность сварных соединений

25. Расчет на прочность паянных соединений

26. От чего зависит прочность клеевого соединения

27. Клеммовые соединения. Конструкции и применение

32. Критерии работоспособности шлицевых соединений. Почему они изнашиваются и как это учитывается при расчете

33. Что такое механическая передача и необходимость ее применения

35. Основные характеристики механических передач:

38. Что такое коэффициент перекрытия зубчатой передачи

39. Что такое контактные напряжения и как они определяются

23. Соединение пайкой. Область применения

28. Виды шпонок

31. В чем преимущества шлицевого соединения по сравнению со шпоночным

34. Классификация механических передач

40. Расчет на прочность зубчатых передач

42. Основной расчет ременной передачи

44. Подшипники, их виды

45. Подшипинки скольжения

49. Проектный расчет вала

50. В чем сущность расчета валов на усталость

51. Как можно повысить сопротивление усталости валов

53. В чем состоит задача расчета на прочность? на жесткость? на устойчивость?

58. Как формулируется закон гука при растяжении? напишите формулы абсолютной и относительной продольных деформаций бруса?

59. Какой случай плоского напряженного состяния называется чистым сдвигом? закон гука при сдвиге?

60. Что такое полярный момент инерции и полярный момент сопротивления? связь между ними

65. Как производится расчет скручиваемого бруса на прочность и жесткость?

66. Какие типы опор применяются для закрепления балок и как направлены их реакции?

67. Как производится расчет на почность при прямом изгибе

71. Что такое система вала и система отверстия

43. Фрикционные передачи

46. Подшипники качения

47. Расчет подшипников качения

54. Какие внутренние усилия могут возникнуть в поперечных сечениях брусьев и какие виды деформаций с ними связаны?

55. В чем сущность метода сечений

61. Что такое осевой момент инерции и осевой момент сопротивления. Связь между ними

62. Какой из двух осевых моментов инерции треугольника больше: относительно оси, проходящей….

63. Что представляют собой эпюры крутящих моментов и как они строятся

68. В каких случаях следует производить дополнительную проверку балок на прочность по наибольшим касательным напряжениям. Как производится эта проверка???

69. Какая дифференциальная зависимость существует между интенсивностью нагрузки, поперечной силой и изгибающим моментом

Схематичное изображение подвижной шарнирной опоры дано на рис. 3.2, б.

Подвижные опоры дают возможность балке беспрепятственно изменять свою длину при изменении температуры и тем самым устраняют возможность появления температурных напряжений.

2. Неподвижная шарнирная опора (рис. 3.2, в). Такая опора допускает вращение конца балки, но устраняет поступательное перемещение ее в любом направлении. Возникающую в ней реакцию можно разложить на две составляющие - горизонтальную и вертикальную.

3. Жесткая заделка, или защемление (рис. 3.2, г). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в общем случае возникать реакция, которую обычно раскладывают на две составляющие (вертикальную и горизонтальную) и момент защемления (реактивный момент).

67. Как производится расчет на почность при прямом изгибе

Условие прочности по нормальным напряжениям

Где – наибольшее по модулю напряжение в поперечном сечении; – изгибающий момент; – осевой момент сопротивления; – допускаемые нормальные напряжения.

Условие прочности по касательным напряжениям

,

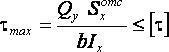где – наибольшее по модулю напряжение в поперечном сечении; – допускаемые касательные напряжения.

Если для материала балки заданы различные допускаемые нормальные напряжения при растяжении и сжатии, то условия прочности применяют отдельно к наиболее растянутым и к наиболее сжатым волокнам балки.

71. Что такое система вала и система отверстия

Стандартами допусков и по­садок в нашей промышленности установлены две возможные к применению совокупности посадок - система отверстия и система вала.

Системой отверстия называется совокупность посадок, в которых предельные отклонения отверстий одинаковы (при одном и том же классе точности и одном и том же номинальном размере), а различные посадки достигаются путем изменения предельных отклонений валов (рис. 73, а). Во всех посадках системы отверстия нижнее предельное отклонение отверстия всегда равно нулю.

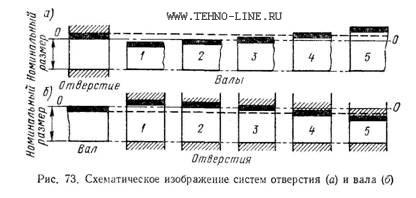
Такое отверстие называется основным отверстием. Из рисунка видно, что при одном и том же номинальном размере (диаметре) и постоянном допуске основного отверстия могут быть получены разные посадки за счет изменения предельных размеров вала. В самом деле, вал 1 даже наибольшего предельного диаметра свободно войдет в наименьшее отверстие. Соединив вал 2 при наибольшем предельном его размере с наименьшим отверстием, мы получим зазор, равный нулю, но при других соотношениях диаметров отверстия и вала в этом сопряжении получается подвижная посадка. Посадки Балов 3 и 4 относятся к группе переходных, так как при одних значениях действительных размеров отверстий и валов 3 и 4 будет иметь место зазор, а при других натяг. Вал 5 при всех условиях войдет в отверстие с натягом, что всегда обеспечит неподвижную посадку.

Основное отверстие в системе отверстия обозначается сокращенно буквой А в отличие от обозначения второй (не основной) детали, входящей в сопряжение, которая обозначается буквами соответствующей посадки.

Системой вала называется совокупность посадок, в которых пре­ельные отклонения валов одинаковы (при одном и том же классе очности и одном и том же номинальном размере), а различные посадки достигаются путем изменения предельных отклонений отверстий. Во всех посадках системы вала верхнее предельное отклонение вала всегда равно нулю. Такой вал называется основным валом.

Схематическое изображение системы вала дано на рис. 73, б,из которого видно, что при одном и том же номинальном размере (диаметре) и постоянном допуске основного вала могут быть получены различные посадки за счет изменения предельных размеров отверстия. Действительно, соединяя с данным валом отверстие 1, мы при всех условиях будем получать подвижную посадку. Подобную же посадку, но с возможным получением зазора, равного нулю, мы получим при сопряжении с данным валом отверстия 2. Соединения вала с отверстиями 3 и 4 относятся к группе переходных посадок, а с отверстием 5 - к неподвижной посадке.

Основной вал в системе вала обозначается сокращенно буквой В.

Иметь представление о видах опор и возникающих реакциях в опорах.

Знать три формы уравнений равновесия и уметь их использо­вать для определения реакций в опорах балочных систем.

Уметь выполнять проверку правильности решения.

Виды нагрузок и разновидности опор

Виды нагрузок

По способу приложения нагрузки делятся на

· сосредоточенные и

· распределенные.

Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосре­доточенной.

Часто нагрузка распределена по значительной площадке или ли­нии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.

В задачах статики для абсолютно твердых тел распределен­ную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 6.1).

q - интенсивность на­грузки; I - длина стержня;

G = ql - равнодей­ствующая распределенной нагрузки.

Разновидности опор балочных систем (см. лекцию 1)

Балка - конструктивная деталь в виде прямого бруса, закреп­ленная на опорах и изгибаемая приложенными к ней силами.

Высота сечения балки незначительна по сравнению с длиной.

Жесткая заделка (защемление) (рис. 6.2)

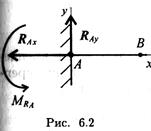Опора не допускает перемещений и поворотов. Заделку заменя­ют двумя составляющими силы Rax и и парой с моментом Mr.

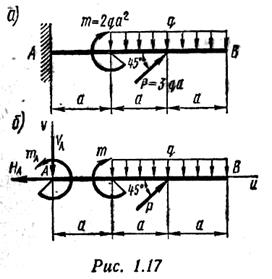
Для определения этих неизвестных удобно использовать систему уравнений в виде

Каждое уравнение имеет одну неиз­вестную величину и решается без подста­новок.

Для контроля правильности решений используют дополни­тельное уравнение моментов относительно любой точки на балке, например

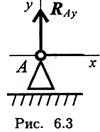
Шарнирно-подвижная опора (рис. 6.3)

Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.

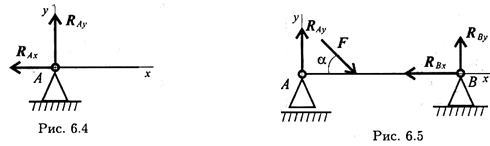
Шарнирно-неподвижная опора (рис. 6.4)

Опора допускает поворот вокруг шарнира и может быть заме­нена двумя составляющими силы вдоль осей координат.

Балка на двух шарнирных опорах (рис. 6.5)

Не известны три силы, две из них - вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй форме:

Составляются уравнения моментов относительно точек крепле­ния балки. Поскольку момент силы, проходящей через точку креп­ления, равен 0, в уравнении останется одна неизвестная сила.

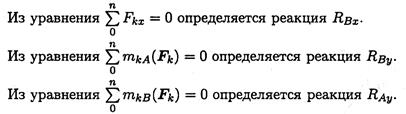
Для контроля правильности решения используется дополни­тельное уравнение

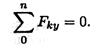
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):

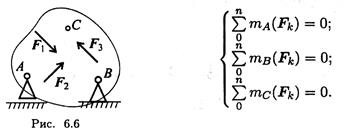
Примеры решения задач

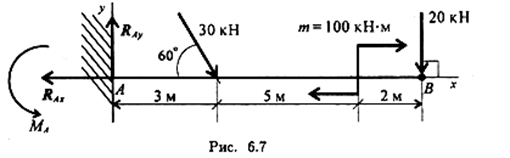
Пример 1. Одноопорная (защемленная) балка нагружена со­средоточенными силами и парой сил (рис. 6.7). Определить реакции заделки.

Решение

2. В заделке может возникнуть реакция, представляемая двум: составляющими (R Ay ,R Ax ), и реактивный момент М A . Наносим на схему балки возможные направления реакций.

Замечание. Если направления выбраны неверно, при расчетах получим отрицательные значения реакций. В этом случае реакции на схеме следует направить в противоположную сторону, не повторяя расчета.

В силу малой высоты считают, что все точки балки находятся на одной прямой; все три неизвестные реакции приложены в одной точке. Для решения удобно использовать систему уравнений равновесия в первой форме. Каждое уравнение будет содержать одну неизвестную.

3. Используем систему уравнений:

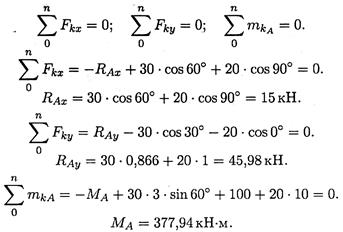
Знаки полученных реакций (+), следовательно, направления ре­акций выбраны верно.

3. Для проверки правильности решения составляем уравнение моментов относительно точки В.

Подставляем значения полученных реакций:

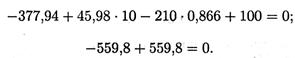
Решение выполнено верно.

Пример 2. Двухопорная балка с шарнирными опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой сил с моментом т (рис. 6.8а). Определить реакции опор.

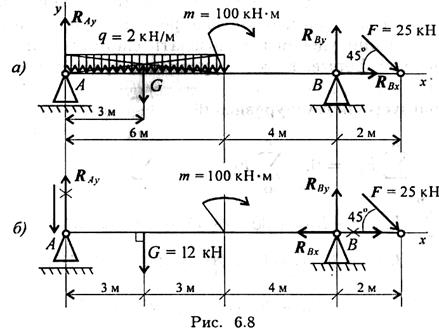Решение

1. Левая опора (точка А) - подвижный шарнир, здесь реакция направлена перпендикулярно опорной поверхности.

Правая опора (точка В) - неподвижный шарнир, здесь наносим две составляющие реакции вдоль осей координат. Ось Ох совмещаем с продольной осью балки.

2. Поскольку на схеме возникнут две неизвестные вертикальные реакции, использовать первую форму уравнений равновесия нецеле­сообразно.

3. Заменяем распределенную нагрузку сосредоточенной:

G = ql; G = 2*6 = 12 кН.

Сосредоточенную силу помещаем в середине пролета, далее за­дача решается с сосредоточенными силами (рис. 6.8, б).

4. Наносим возможные реакции в опорах (направление произвольное).

5. Для решения выбираем уравнение равновесия в виде

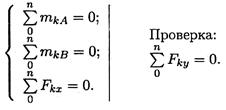
6. Составляем уравнения моментов относительно точек крепления:

Реакция отрицательная, следовательно, R А y нужно направить н противоположную сторону.

7. Используя уравнение проекций, получим:

R Bx - горизонтальная реакция в опоре В.

Реакция отрицательна, следовательно, на схеме ее направление будет противоположно выбранному.

8. Проверка правильности решения. Для этого используем чет­вертое уравнение равновесия

Подставим полученные значения реакций. Если условие выполнено, решение верно:

5,1 - 12 + 34,6 – 25 -0,7 = 0.

Пример 3. Опреде­лить опорные реакции балки, показанной на рис. 1.17, а .

Решение

Рассмотрим рав­новесие балки АВ. Отбросим опорное закрепление (задел­ку) и заменим его действие реакциями Н А, V A и т А (рис. 1.17, б ). Получили плоскую систему произвольно распо­ложенных сил.

Выбираем систему координат (рис. 1.17,6) и состав­ляем уравнения равновесия:

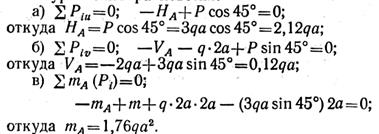
Составим проверочное уравнение

следовательно, реакции определены верно.

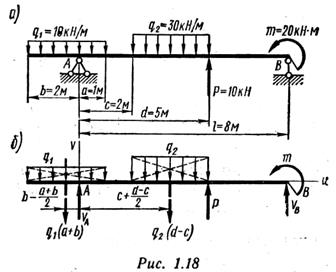Пример 4. Для заданной балки (рис. 1.18, а ) определить опорные реакции.

Решение

Рассматриваем равновесие балки АВ. Отбра­сываем опорные закрепления и заменяем их действие реакциями (рис. 1.18,6). Получили плоскую систему про­извольно расположенных сил.

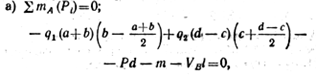
Выбираем систему координат (см. рис. 1.18,6) и со­ставляем уравнения равновесия:

q 1 ,

Расстояние от точки А q 1 (а + b);

Равнодействующая равномерно распреде­ленной нагрузки интенсивностью q 2 ;

Расстояние от точки А до линии действия равнодействующей q 2 (d - с).

Подставив числовые значения, получим

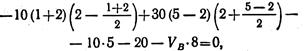
откуда V B = 28,8 кН;

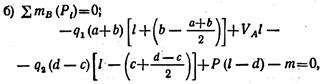
- расстояние от точки В до линии действия равнодействующей q 1 (a+b);

- расстояние от точки В до линии действия равнодействующей q 2 (d - c).

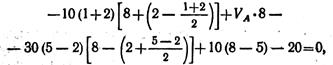
откуда V A = 81,2 кН.

Составляем проверочное уравнение:

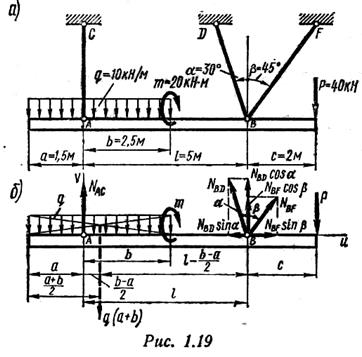
Пример 5. Для заданной стержневой системы (рис. 1.19, а ) определить усилия в стержнях.

Решение

Рассмотрим равновесие балки AB, к которой приложены как заданные, так и искомые силы.

На балку действуют равномерно распределенная на­грузка интенсивностью q, сила Р и сосредоточенный мо­мент т .

Освободим балку от связей и заменим их действие реакциями (рис. 1.19, б ). Получили плоскую систему про­извольно расположенных сил.

Выбираем систему координат (см. рис. 1.19, б ) и со­ставляем уравнения равновесия:

Где q (a + b) - равнодействующая

равномерно распреде­ленной нагрузки интенсивностью q (на чертеже она показана штриховой ли­нией).

Подставив числовые значения, получим:

откуда N AC = 16 кН;

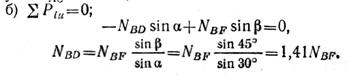
Напомним, что сумма проекций сил, образующих пару, на любую ось равна нулю;

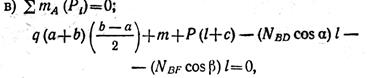
где N BD cos α N BD ", N BF cos β - вертикальная составляющая силы N BF (линии действия горизонтальных состав­ляющих сил N BD и N BF проходят через точку А и поэтому их моменты относи­тельно точки А равны нулю). Подставляя числовые значения и учитывая, что N BD = 1,41 N BF , получаем:

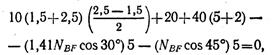
откуда N BF = 33,1 кН.

Тогда N BD = 1,41*33,1 = 46,7 кН.

Для определения усилий в стержнях не было исполь­зовано уравнение равновесия: ΣP to = 0. Если усилия в стержнях определены верно, то сумма проекций на ось v всех сил, действующих на балку, должна быть равна нулю. Проектируя все силы на ось v, получаем:

следовательно, усилия в стержнях определены верно.

Пример 6. Для заданной плоской рамы (рис. 1.20, а ) определить опорные реакции

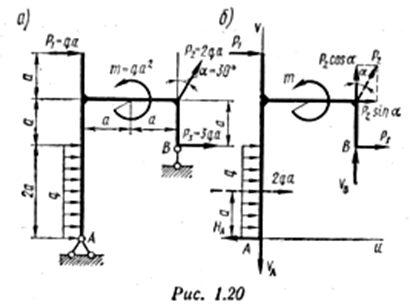
Решение

Освобождаем раму от связей и заменяем их действие реакциями N А, V A , V B (рис. 1.20, б ). Получили плоскую систему произвольно расположенных сил.

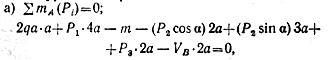
Выбираем систему координат (см. рис. 1.20, б ) и составляем уравнения равновесия:

где Р 2 cos α - вертикальная составляющая силы Р 2 ;

P 2 sin α - горизонтальная составляющая силы Р 2 ;

2qa - равнодействующая равномерно распределенной нагрузки интенсивностью q (показана штриховой линией);

откуда V B = 5,27qa;

откуда H A =7qa

линия действия силы Р 2 cosα проходит через точку В и поэтому ее момент относительно точки В равен нулю

откуда V A = 7qa.

Для определения реакций не было использовано урав­нение равновесия ΣP iv =0. Если реакции определены верно, то сумма проекций на ось v всех сил, действую­щих на раму, должна быть равна нулю. Проектируя все силы на ось v, получаем:

следовательно, опорные реакции определены верно.

Напомним, что сумма проекций сил, составляющих пару с моментом т, на любую ось равна нулю.

Контрольные вопросы и задания

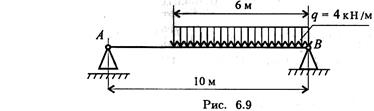
1. Замените распределенную нагрузку сосредоточенной и опре­делите расстояние от точки приложения равнодействующей до опо­ры А (рис. 6.9).

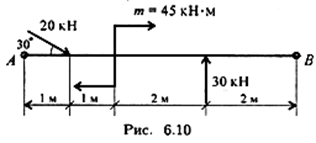
2. Рассчитайте величину суммарного момента сил системы от­носительно точки А (рис. 6.10).

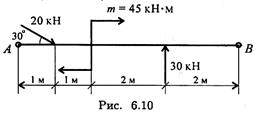
3. Какую из форм уравнений равновесия целесообразно исполь­зовать при определении реакций в заделке?

4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?

5. Определите реактивный момент в заделке одноопорной балки, изображенной на схеме (рис. 6.11).

6. Определите вертикальную реакцию в заделке для балки, представленной на рис. 6.11.

Лекция №3

Тема: « Внутренние усилия в поперечных сечениях стержня»

Вопросы:

1. Опоры и опорные реакции, и их определение

3. Взаимосвязь между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки

1. Опоры и опорные реакции, и их определение

При расчете конструкций в основном встречаются элементы, испытывающие изгиб. Стержни, работающие преимущественно на изгиб, называют балками. Для того чтобы балка могла испытывать нагрузку и передавать ее на основание, она должна быть соединена с ним опорными связями. На практике применяют несколько типов опорных связей, или, как говорят, несколько типов опор.

Различают три основных типа опор:

а) шарнирно-подвижная опора:

б) шарнирно-неподвижная опора:

в) жесткая заделка.

Рис. 1

На рис. 1 показана шарнирно-подвижная опора, такая опора позволяет балке свободно поворачиваться и перемещаться в горизонтальном направлении. Поэтому реакция в опоре будет одна  вертикальная сила. Условное обозначение такой опоры показано справа.

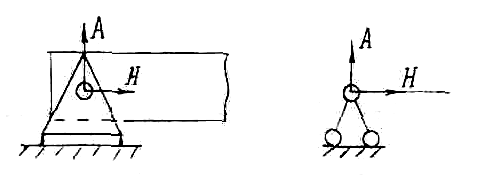
Рис. 2

На рис. 2 показана шарнирно-неподвижная опора. Такая опора позволяет балке свободно поворачиваться, но перемещаться она не может. Поэтому могут возникать две реакции - вертикальная и горизонтальная силы. Их можно сложить и получить одну результатирующую силу, но нужно знать угол, под которым oна будет направлена. Более удобно будет пользоваться вертикальной и горизонтальной составляющими реакции.

На рис. 3 показана жесткая заделка. Она не позволяет балке ни поворачиваться, ни перемещаться. Поэтому могут возникать три опорные реакции: момент, вертикальная и горизонтальная силы. Если балка не имеет на конце опоры, то эта часть ее называется консолью.

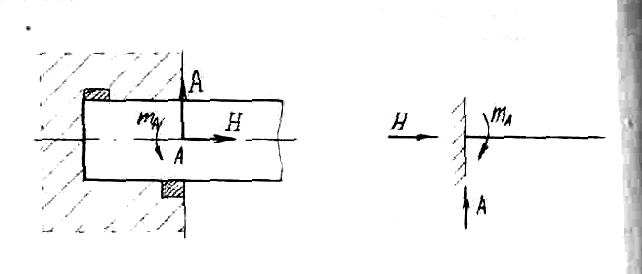
Рис. 3

Определим реакции опор для балки (см. рис. 4).

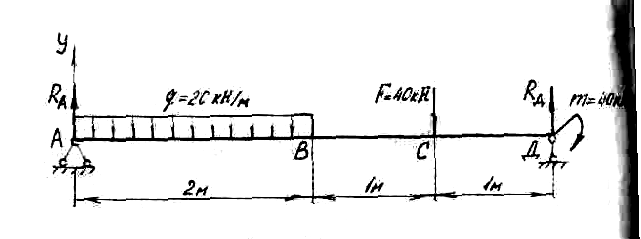
Рис.4

В опоре А горизонтальная реакция равна нулю, так как распределенная нагрузка q и сосредоточенная сила F имеют вертикальное направление. Реакции опор

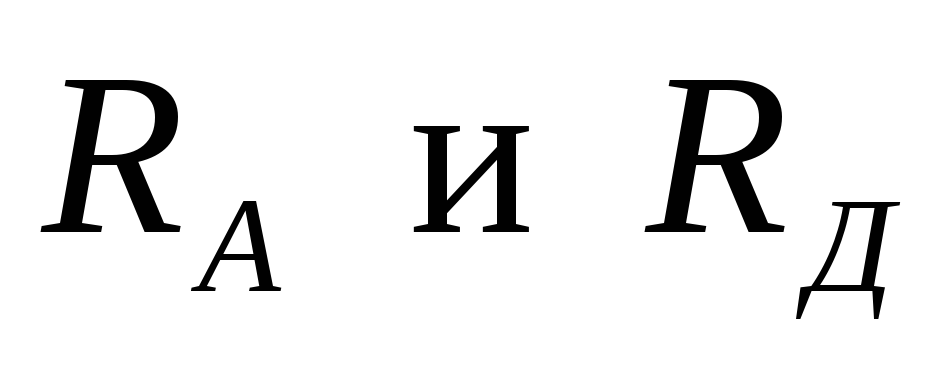направим вверх. Составим два уравнения статического равновесия сил. Сумма моментов относительно каждой из опор равна нулю. Уравнения моментов нужно составлять относительно опор, так как в этом случае получаются уравнения с одним неизвестным. Если составить уравнения относительно точек В и С, то получим уравнения с двумя неизвестными, а их решать сложнее. Моменты против часовой стрелки будем считать положительными, по часовой  отрицательными.

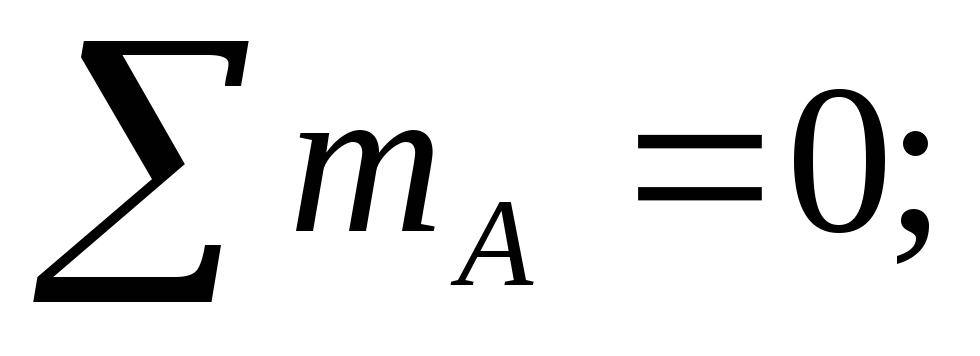
где

 момент от равномерно распределенной нагрузки.

Произведение q на расстояние, на котором она приложена, из условия равновесия системы равно сосредоточенной силе, приложенной посредине отрезка. Поэтому момент

равен:

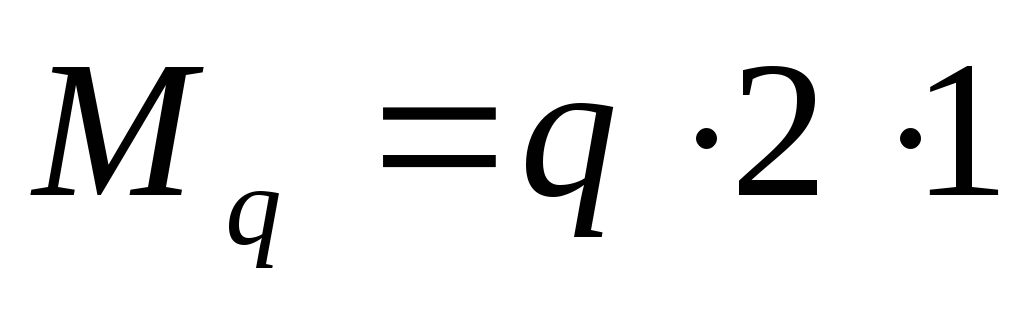
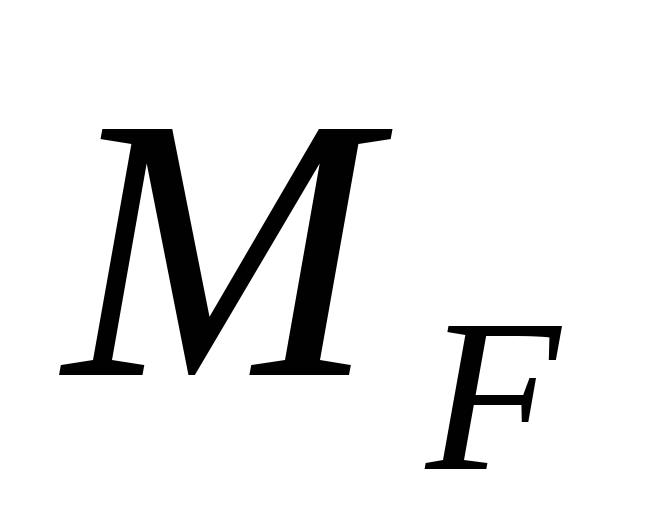–момент силы F

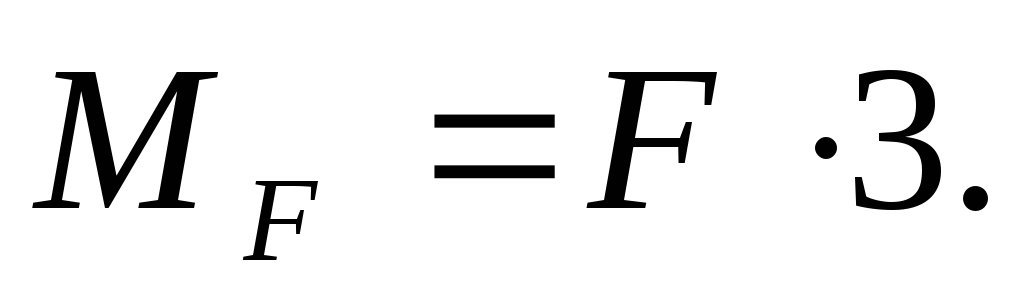
Внешний момент m на плечо не умножается, так какэто пара сил, т.е. две равные по величине, противоположно направленные силы, имеющие постоянное плечо.

.

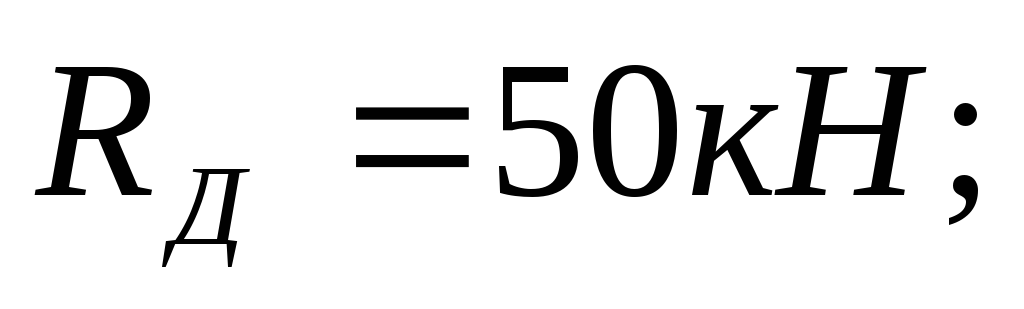
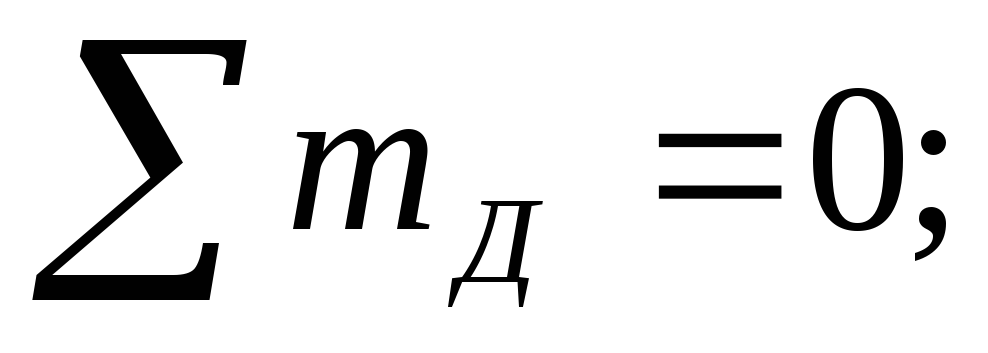
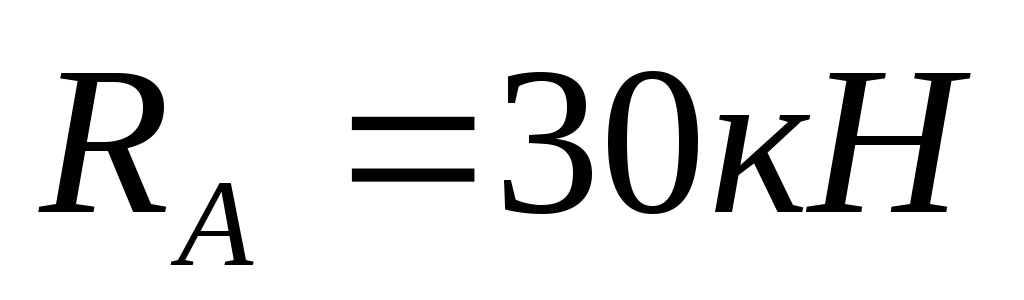Проверка: Сумма всех сил на вертикальную ось Y должна быть равна нулю:

.

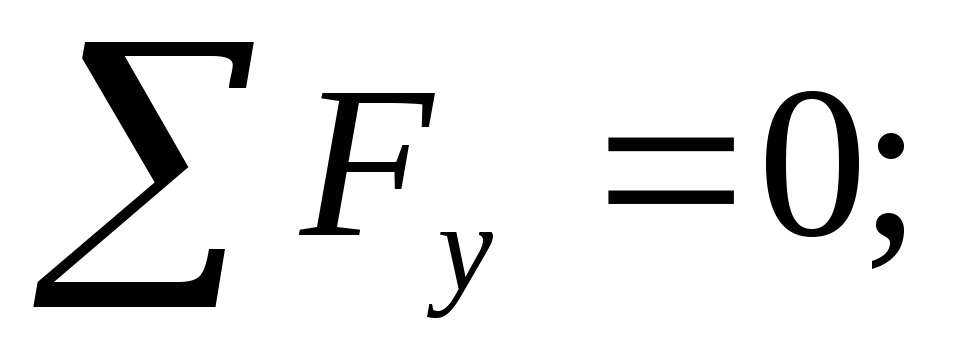
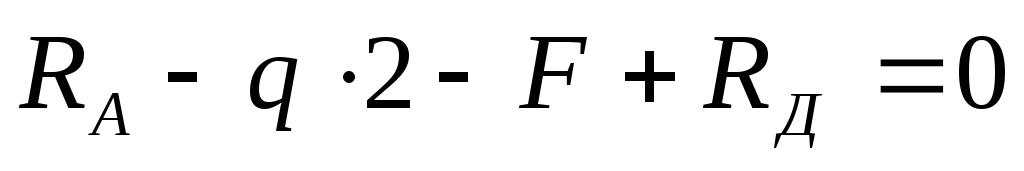Момент m в условие статического равновесия

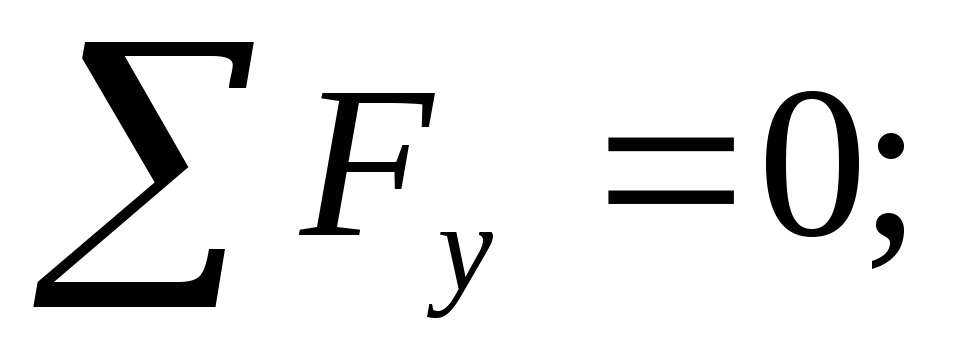не записывают, так как момент  это две равные по величине, противоположно направленные силы и в проекции на любую ось они дадут ноль.

30-20-2-40+50=0:

80-80=0.

Реакции определены правильно.

2. Поперечная сила и изгибающий момент

Пусть на балку действуют силы

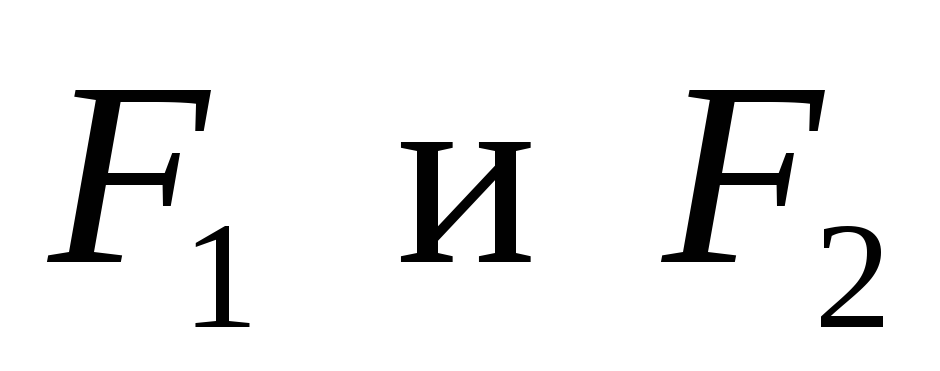, реакции опор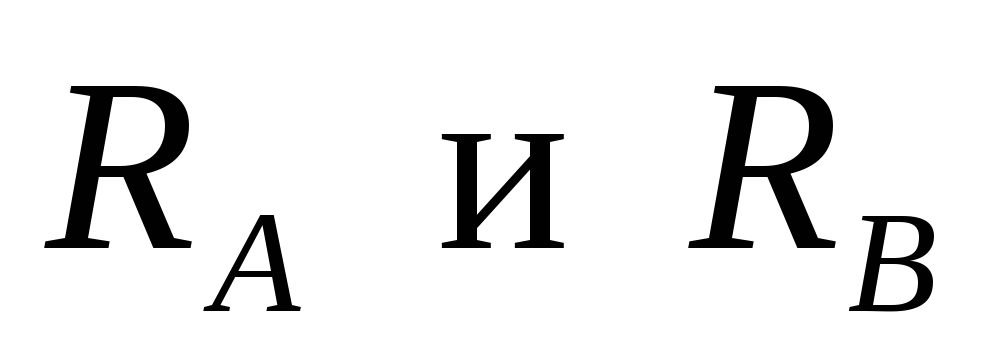

. Определим внутренние усилия в сечении, расположенном на расстоянии от нулевого конца (см. рис.5).

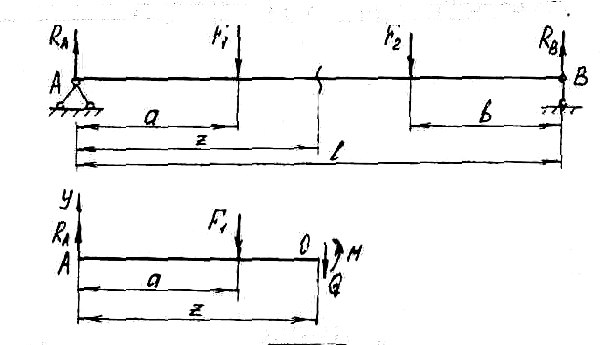
Рис. 5

Поскольку все внешние силы действуют вертикально, то горизонтальной составляющей у реакции опоры А не будет. Балка не будет сжиматься или растягиваться, т.е. продольная сила в поперечных сечениях равна нулю. Можно было взять пример, когда силы

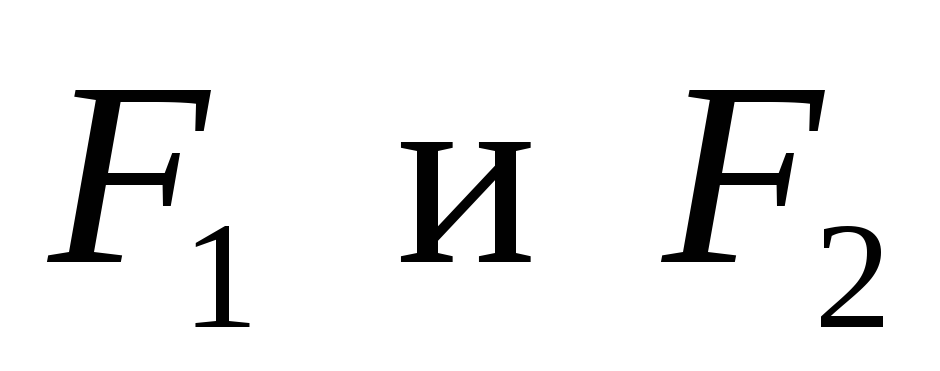были бы не вертикальными по направлению. Тогда бы в опоре А была бы и вторая реакция  горизонтальная сила, а в сечениях балки  продольная сила N . В этом случае балка испытывала бы изгиб с растяжением (сжатием), т.e. был бы случай сложного сопротивления. Его мы будем изучать позднее. Вначале рассматривают более простые задачи и идут к более сложным, а не наоборот.

Поскольку внешние силы

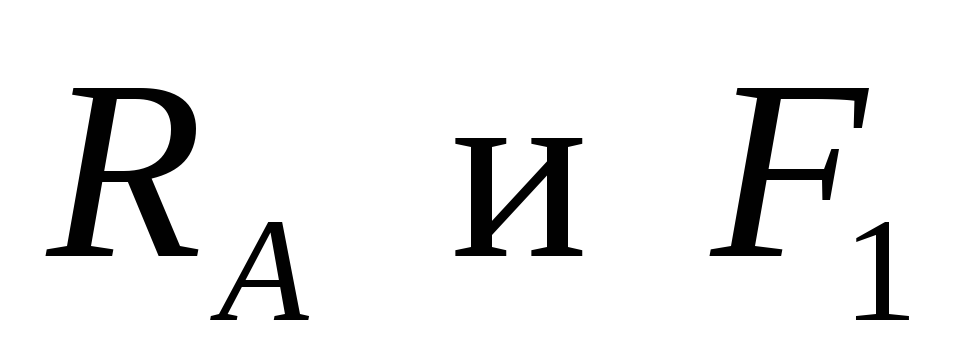лежат в одной плоскости, проходящей через ось бруса, то возможно возникновение тpex внутренних усилий: изгибающею момента М , поперечной силы Q и продольной силы N , которая, как мы отмечали, равна нулю. Значения М и Q определим из уравнения статического равновесия левой части балки:

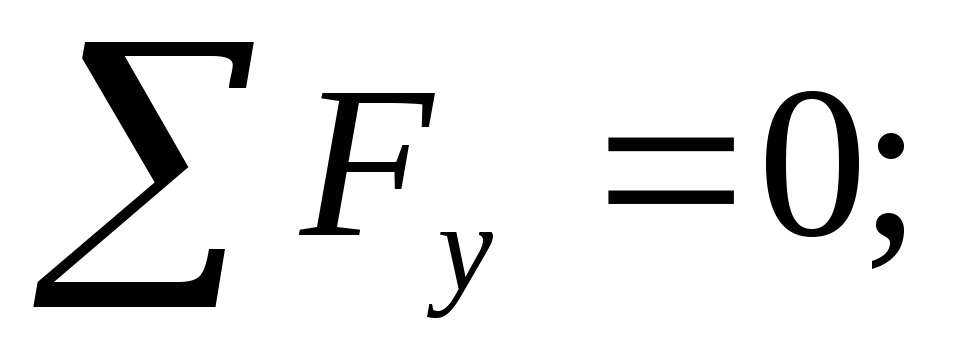
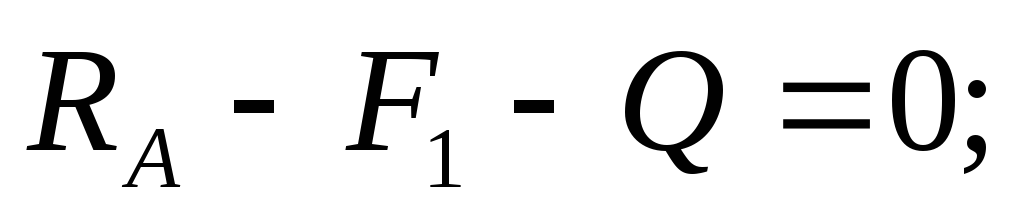
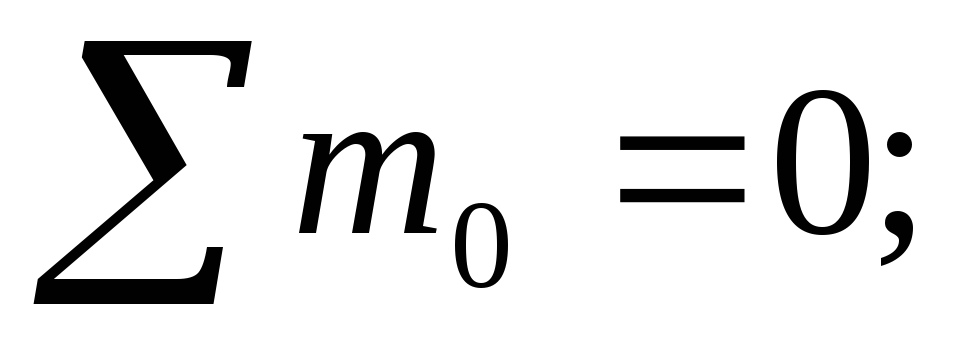
Вывод: поперечная сила в сечении численно равна алгебраической сумме всех внешних сил, а изгибающий момент  сумме всех моментов, вычисленных относительно сечения и приложенных к рассматриваемой части балки.

Для поперечных сил и изгибающих моментов приняты обязательные правила знаков (см. рис. 6).

Если сила пытается повернуть рассматриваемую часть балки по часовой стрелке, то она вызывает положительную поперечную силу, и, наоборот, если действует против часовой стрелки  то поперечная сила отрицательная. На рис. 5 сила

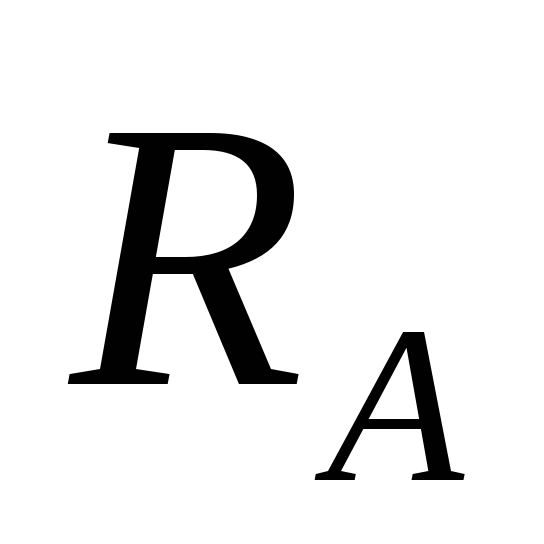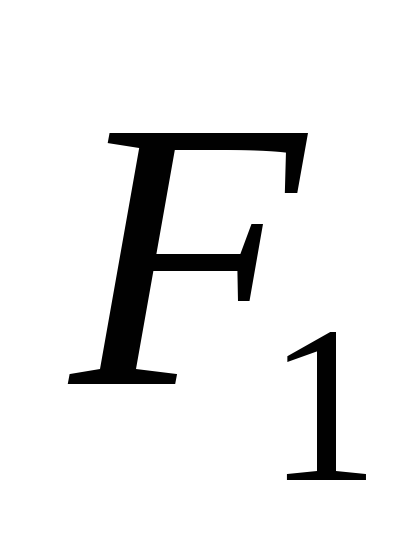
вызывает положительное Q , а  отрицательное. Следует отметить, что направление силы положительное для левой части будет отрицательным для правой части. Это вызвано тем, что внутренние силы, действующие на правую и левую часть балки обязательно должны быть равны и противоположно направлены.

Если внешняя сила или внешний момент изгибают балку выпуклостью вниз, то возникающий изгибающий момент положительный и, наоборот, выпуклостью вверх  отрицательный.

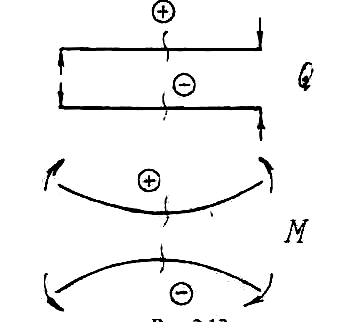
Рис. 6

3. Взаимосвязь между изгибающим моментом,

поперечной силой и интенсивностью распределенной нагрузки

Пусть на консольную балку (см. рис. 7) действует распределенная нагрузка, изменяющаяся по длине балки. На расстоянии z от левого конца возьмем бесконечно малый отрезок dz .

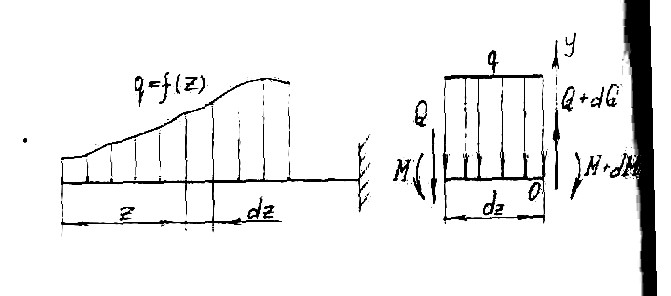
Рис. 7

Тогда распределенную нагрузку на нем можно рассматривать как постоянную. В левой части рассматриваемого отрезка будут внутренние усилия Q и М , в правой  с учетом приращения внутренних усилий Q + dQ и M + dM .

Составим уравнения статического равновесия для отрезка балки:

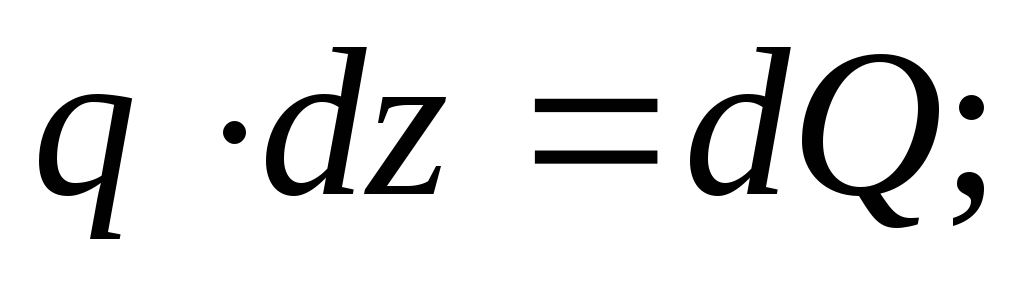
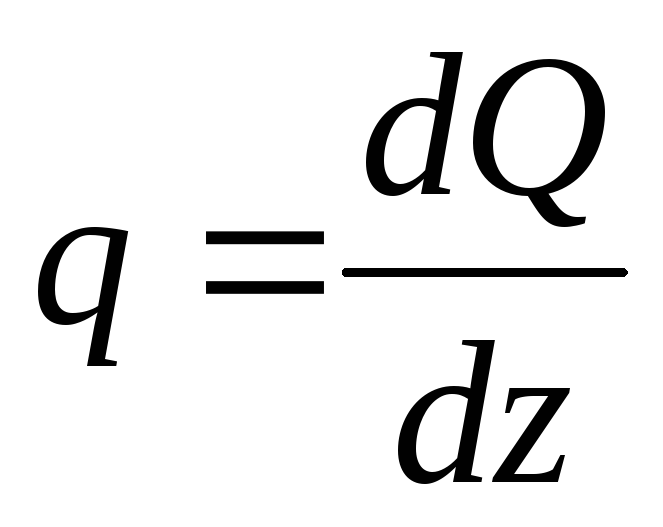(1)

Третьим членом можно пренебречь, как бесконечно малой величиной более высокого порядка, т.е.:

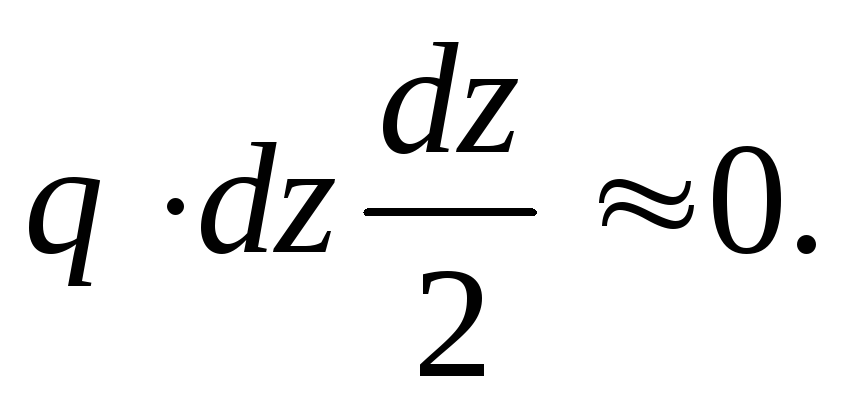
После преобразований получим:

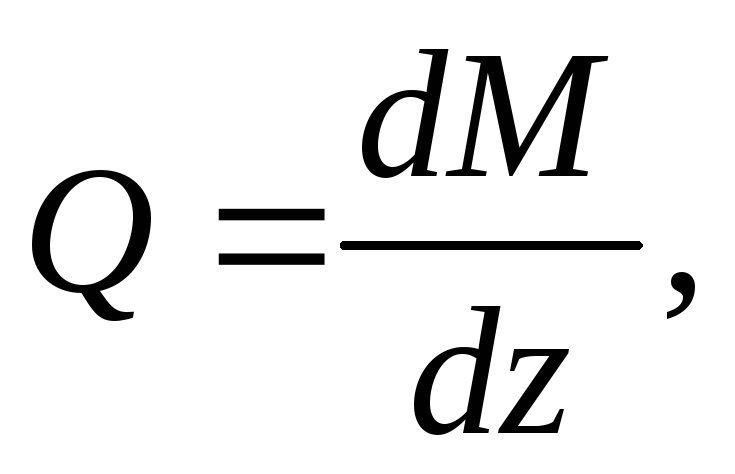(2)

т.е. первая производная от изгибающего момента по абсциссе (длине балки) есть поперечная сила.

Если в формулу (1) подставить значение Q из формулы (2), то получим:

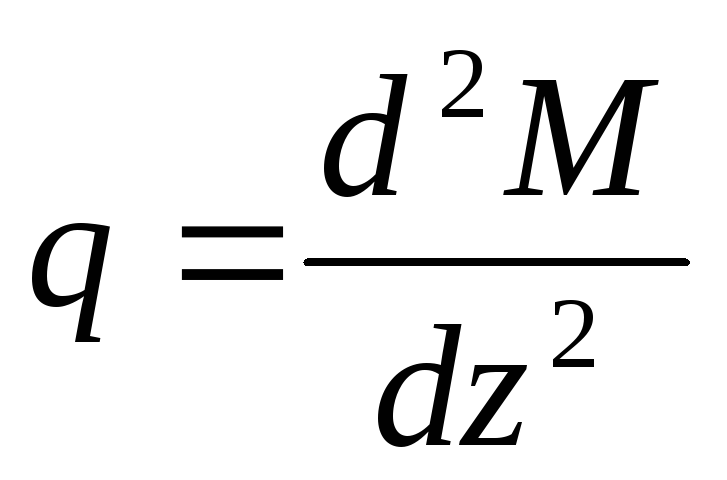, (3)

т.е. вторая производная от изгибающего момента есть интенсивность распределенной нагрузки.

Пространственное твердое тело имеет шесть степеней свободы перемещений - три поступательных движения и три вращательных вокруг трех взаимно перпендикулярных осей. Плоское тело имеет только три степени свободы - два поступательных движения в направлении двух осей и вращение вокруг третьей оси. Опорные устройства препятствуют тем или иным из указанных перемещений тела или вообще исключают всякое его движение. Опорные устройства классифицируются по числу связей, накладываемых на перемещения опорных точек (узлов) тела. Связь обычно представляют в виде стержня, соединяющего тело с опорной поверхностью. Если нет специального указания, опорные связи и поверхности считаются абсолютно жесткими.

При нагружении тела на него со стороны опорных связей начинают действовать силы, называемые опорными реакциями. Опорные реакции находятся из уравнений равновесия тела, у которого опорные связи мысленно удалены и заменены силами, направленными вдоль снятых связей.

Для плоского тела, и в частности для плоского бруса, основными видами опор являются шарнирно-подвижная , шарнирно-неподвижная и защемляющая неподвижная .

Шарнирно-подвижная , или, иначе, катковая опора исключает перемещение опорного узла А в направлении, перпендикулярном опорной поверхности, но не препятствует вращению тела вокруг опорной точки и поступательному перемещению параллельно опорной поверхности. Такой опоре соответствует одна опорная реакция, направленная перпендикулярно опорной поверхности. Схематические изображения катковой опоры представлены на рис. 1.3. Там же показано направление опорной реакции.

Рис. 1.3. Шарнирно-подвижная опора

Шарнирно-неподвижная , или, короче, шарнирная опора исключает всякое поступательное движение опорного узла A , но не препятствует вращению тела вокруг опорной точки. Реакцию такой опоры, направление которой заранее неизвестно, принято раскладывать на две составляющие R x и R y , направленные по касательной и нормали к опорной поверхности, как показано на рис. 1.4. На этом же рисунке представлены схематические изображения шарнирных опор.

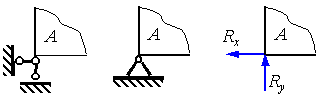
Рис. 1.4. Шарнирно-неподвижная опора

Защемляющая неподвижная опора , или, иначе, заделка (рис. 1.5) исключает поступательные и вращательные движения тела. В соответствии с тремя связями, накладываемыми на тело, реакциями заделки являются силы R x и R y и опорный момент M . Конструктивное оформление опорных устройств каждого из указанных типов отличается большим разнообразием. В приведенных на рис. 1.3, 1.4 и 1.5 общепринятых схематических изображениях опор подчеркиваются их самые характерные особенности.

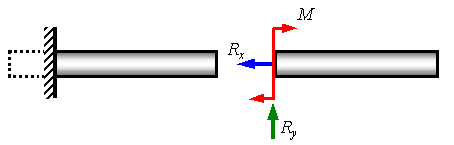
Рис. 1.5. Неподвижная опора